

|
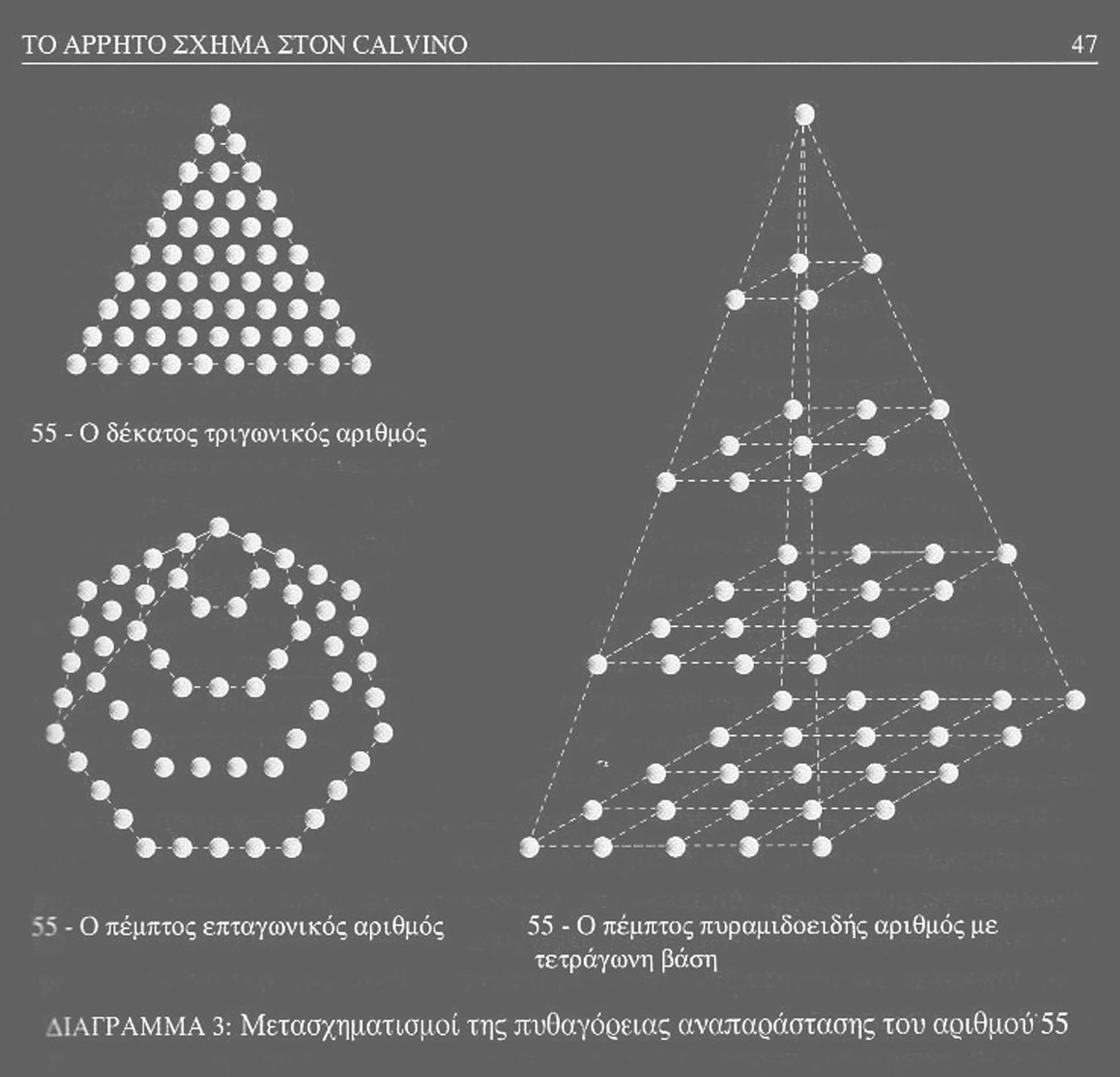
Και καταλαβαίνουμε τώρα γιατί είναι 55 οι αόρατες πόλεις. Γνωρίζουν ότι οι Πυθαγόρειοι αναπαριστούσαν τους αριθμούς με την τοποθέτηση στιγμάτων κατά μήκος γραμμών, έτσι ώστε να σχηματίζονται κανονικά σχήματα. Οι αριθμοί χωρίζονται σε ομάδες ανάλογα με το αν μπορούν να αναπαρασταθούν ως τρίγωνα, τετράγωνα ή άλλα σχήματα (Greek Mathematics, 1939, σελ 86-99). Ο αριθμός 55 εθεωρείτο ιδιαίτερα σημαντικός διότι μπορούσε να αναπαρασταθεί κατά τρεις τρόπους, ως ο δέκατος τρίγωνος αριθμός, ο πέμπτος επτάγωνος αριθμός ή ο πέμπτος πυραμιδοειδής αριθμός με τετράγωνη βάση, όπως φαίνεται στο διάγραμμα 3. Ο αριθμός 55 λοιπόν παραπέμπει ακριβώς στην ιδέα του μετασχηματισμού, διαμέσου της αντιστοιχίας του με πολλά σχήματα. Πεπονής, Γ. (1997). Χωρογραφίες-Ο αρχιτεκτονικός σχηματισμός του νοήματος. Αθήνα: Εκδόσεις Αλεξάνδρεια. σελ. 46
|
|
A beautiful mind. (2001). Σκηνοθέτης: Ron Howard. 1ο απόσπασμα (01:29-02:20 ) Πλοκή: Έτος 1947 κι ο John Nash σε ηλικία μόλις 22 ετών, σπουδαστής στο Princeton, θα καταπλήξει τους πάντες με το εκπληκτικό του ταλέντο στα μαθηματικά. Ευφυής, αλλά χωρίς ικανότητα ν' αναπτύξει κοινωνική ζωή, κυριευμένος από την εμμονή του να βρει μια ιδέα πραγματικά νεωτεριστική. Σύντομα προάγεται σε διδάκτορα, ανατρέποντας μια θεωρία του Adam Smith, πατέρα της μοντέρνας οικονομίας και βρίσκει μια θέση στο MIT. Την ίδια εποχή συνεργάζεται σε κυβερνητικές υπηρεσίες αποκωδικοποιώντας μυστικούς κώδικες, ενώ γνωρίζει την Alicia με την οποία και παντρεύεται. Όμως μέσα σε σύντομο χρονικό διάστημα η περίοδος ευτυχίας θα τελειώσει, ξεκινώντας μια άλλη, γεμάτη παρανοϊκές ψευδαισθήσεις που θα οδηγήσουν στη διάγνωση της σχιζοφρένειας και σε εκτεταμένες θεραπείες. |
| Έστω λοιπόν ότι οι 55 πόλεις μπορούν να κατασκευαστούν ως υλικά τεχνήματα περιορισμένης κλίμακας. Με ποιον τρόπο μπορούν να διαταχθούν στον χώρο έτσι ώστε η λογική της αφήγησης να τραπεί σε περίπατο ενώ η χωροθέτηση να εκφράζει τις αφαιρετικές αρχές που διέπουν τις σχέσεις των πόλεων μέσα στο κείμενο; Μπορούμε για παράδειγμα να προτείνουμε τη διάταξη που παρουσιάζεται στο διάγραμμα 4. Εδώ, οι πέντε πόλεις που απαρτίζουν κάθε θεματική ενότητα τοποθετούνται στις κορυφές ενός νοερά χαραγμένου κανονικού πενταγώνου, και οι έντεκα ενότητες διατάσσονται ως ομόκεντρα πεντάγωνα, εγγεγραμμένα το ένα μέσα στο άλλο. Η διαδοχή των σελίδων αντιστοιχεί στο ξεδίπλωμα ενός τοίχου. Με τρεις εξαιρέσεις, που σημειώνονται ως κολώνες, οι πόλεις βρίσκονται όλες τοποθετημένες στις γωνίες του τοίχου, εκεί που η πορεία αλλάζει φορά. |

|
Σε αυτή την κατασκευή, το ξεδίπλωμα του τοίχου ακολουθεί πιστά τη σειρά του βιβλίου. Η πενταγωνική, όμως. θεμελίωση του σχήματος και η αναπαράσταση των θεματικών ενοτήτων γίνεται περισσότερο σαφής σε όσους κοιτούν τη διαγραμματική κάτοψη και λιγότερο σε εκείνους που επιχειρούν την πραγματική της εσωτερική εξερεύνηση. Η κατασκευή έχει, δηλαδή, μια γεωμετρική συνοχή που είναι λογικά κατανοήσιμη αλλά όχι και αισθησιακά πραγματοποιημένη. Μια εναλλακτική κατασκευή παρουσιάζεται στο διάγραμμα 5. Εδώ οι 55 πόλεις αντιστοιχούν σε δωμάτια που τοποθετούνται επί ορθοκανονικού κανάβου, έτσι ώστε οι πέντε πόλεις κάθε θεματικής ενότητας να είναι οριζόντια στοιχημένες. Κάθε δωμάτιο διασχίζεται από δύο άξονες κίνησης. Η πορεία του βιβλίου αναπαριστάνεται με μια διακεκομμένη γραμμή και ακολουθεί τους κάθετους άξονες. Η εναλλακτική ανάγνωση κατά θεματικές ενότητες μπορεί να αναπαρασταθεί από μια οριζόντια κίνηση. Το σύνολο της διάταξης μοιάζει με Ιπποδάμεια πόλη, σαν τη Νέα Υόρκη που προτιμά ο Calvino λόγω της γεωμετρικότητάς της και της έλλειψης βάθους (Calvino, 1990). Η ενότητα περί πόλεων και ματιών αναπαριστάνεται ως ξεχωριστή σειρά δωματίων που διαιρεί τη συνολική διάταξη σε δύο ομάδες, των 25 πόλεων η κάθε μια, στοιχημένες σε πέντε γραμμές. Στη δεύτερη διάταξη οι πορείες είναι πιο ελεύθερες απ' ότι στην πρώτη και η συντακτική δομή είναι πιο ευανάγνωστη. Όμως η γεωμετρική χάραξη είναι λιγότερο περίτεχνη. Έτσι, η διαφορά ανάμεσα στις δύο εναλλακτικές συνθέσεις συνδέεται με τη βασική διαλεκτική του ορισμού του αρχιτεκτονικού χώρου, αφενός ως διάταξης περιπατητικώς εξερευνήσιμης και κατανοήσιμης και αφετέρου ως γεωμετρική σύνθεσης, η λογική συνέπεια της οποίας τρέπεται σε αντικείμενο εσωτερικού στοχασμού. Και αν η μαγεία της πόλης είναι η έκπληξη που αποκαλύπτει ο περίπατος και συγκαλύπτει το σχέδιο, η τέχνη της αρχιτεκτονικής έγκειται στο να προσφερθεί τούτη η έκπληξη της συνθετικής σύλληψης ως περιπατητική ποιότητα. Προς την κατεύθυνση αυτή του διαλόγου θα μπορούσε να αναζητηθεί η παραλληλία ανάμεσα στη λογοτεχνική και σε μιαν άλλη, οικοδομική τούτη τη φορά, αρχιτεκτονική των Πόλεων της Γραφής. Πεπονής, Γ. (1997). Χωρογραφίες- Ο αρχιτεκτονικός σχηματισμός του νοήματος. Αθήνα: Εκδόσεις Αλεξάνδρεια. σελ. 51-52 |

| Kliment Redko (1897-1956). Φωτογραφία από το βιβλίο: Καφετσή, Α. (Επιμ.) (1995). Ρώσικη πρωτοπορία 1910-1930- Η συλλογή Κωστάκη. Υπουργείο Πολιτισμού, Εθνική Πινακοθήκη και Μουσείο Αλέξανδρου Σούτσου, Ευρωπαϊκό Πολιτιστικό Κέντρο Δελφών. σ. 431 |
|
|
Red'ko or Redko Kliment (Ρέντκο, Kλίμεντ) Ζωγράφος (Πολωνία 1897-Μόσχα 1956) Το 1910 γράφτηκε στη Σχολή Αγιογραφίας της μονής Κίεβο –Πετσέρσκ με δάσκαλο τον Α. Τζιζέφσκι. Παρακολούθησε μαθήματα στη Σχολή της Εταιρείας για την Προώθηση των Τεχνών της Πετρούπολης (1914-15). Το 1918 μετοίκησε στο Κίεβο και παρακολούθησε μαθήματα στην Καλλιτεχνική Ακαδημία της Ουκρανίας και πήρε μέρος στη διακόσμηση της πόλης για τον εορτασμό της Επανάστασης. Το 1920 πήγε στη Μόσχα όπου παρακολούθησε μαθήματα στα Βχουτέρας (1920-22). Μετά από μια σύντομη σουπρεματιστική περίοδο που κράτησε μέχρι το τέλος του 1921, υιοθέτησε στη ζωγραφική του τους «μηχανικούς οργανισμούς». Πρωτοστάτησε στην ίδρυση της ομάδας «Ηλεκτροοργανισμός». Η ομάδα διοργάνωσε μια έκθεση στο Μουσείο Ζωγραφικής Παιδείας της Μόσχας το 1922. Πρώτη έκθεση ρωσικής τέχνης στο Βερολίνο το 1922 και στην Πετρούπολη το 1923. Χαρακτήρισε το έργο του από το 1923 έως το 1924 ως «λουμινιστικό». Το 1924 συμμετείχε στη Πρώτη διαλογική έκθεση των ενώσεων δραστικής επαναστατικής τέχνης στη Μόσχα. Στο κατάλογο υπέγραψε τη διακήρυξη των «Προβολιστών». Από το 1927 έως το 1935 έζησε στο Παρίσι. Ήταν μέλος της ομάδας ουκρανών καλλιτεχνών του Παρισιού και της Ένωσης Επαναστατικών καλλιτεχνών της Γαλλίας. Από το 1935 μέχρι το θάνατό του έζησε στη Μόσχα και ζωγράφιζε ρεαλιστικά. |
|
A beautiful mind. (2001). Σκηνοθέτης: Ron Howard. 2ο απόσπασμα (10:06-11:20) Πλοκή: Έτος 1947 κι ο John Nash σε ηλικία μόλις 22 ετών, σπουδαστής στο Princeton, θα καταπλήξει τους πάντες με το εκπληκτικό του ταλέντο στα μαθηματικά. Ευφυής, αλλά χωρίς ικανότητα ν' αναπτύξει κοινωνική ζωή, κυριευμένος από την εμμονή του να βρει μια ιδέα πραγματικά νεωτεριστική. Σύντομα προάγεται σε διδάκτορα, ανατρέποντας μια θεωρία του Adam Smith, πατέρα της μοντέρνας οικονομίας και βρίσκει μια θέση στο MIT. Την ίδια εποχή συνεργάζεται σε κυβερνητικές υπηρεσίες αποκωδικοποιώντας μυστικούς κώδικες, ενώ γνωρίζει την Alicia με την οποία και παντρεύεται. Όμως μέσα σε σύντομο χρονικό διάστημα η περίοδος ευτυχίας θα τελειώσει, ξεκινώντας μια άλλη, γεμάτη παρανοϊκές ψευδαισθήσεις που θα οδηγήσουν στη διάγνωση της σχιζοφρένειας και σε εκτεταμένες θεραπείες. |
|